再帰的アルゴリズム

再帰

　ある事象は、それが自分自身を含んでいたり、それを用いて定義されているとき、再帰的であるといわれます。

整数の階乗値を求める

　整数nの階乗は以下のように再帰的に定義されます。
　　　　(a) 0! = 1
　　　　(b) n > 0ならば n! = n × (n - 1)!
たとえば、10の階乗である10!は、(b)によって
　　　　10! = 10 × 9!
と求めることができます。もちろん、右辺の9!は、
　　　　9! = 9 × 8!
によって得られます。一般的に表現するために、nの階乗を求める手続きをfactorial(n)とすると、10!および9!は、次のようになります。
　　　　10! = 10 × factorial(9)
　　　　9! = 9 × factorial(8)
すなわち、factorial(n)は、nとfactorial(n - 1)を掛け合わせたものです。したがって、factorial(n - 1)の値がわかれば、容易に計算できることになります。
　このような考え方をもとにして、関数factorialを実現したのが以下に示すプログラムです。

/*
    階乗を求める
*/

#include  <stdio.h>

/*--- 階乗値を返す ---*/
int factorial(int n)
{
    if (n > 0)
        return (n * factorial(n - 1));
    else
        return (1);
}

int main(void)
{
    int  num;

    printf("整数を入力してください：");
    scanf("%d", &num);

    printf("その数の階乗は%dです。\n", factorial(num));

    return (0);
}

　たとえば、3!を求めるのであれば、ひとこと
　　　　factorial(3)
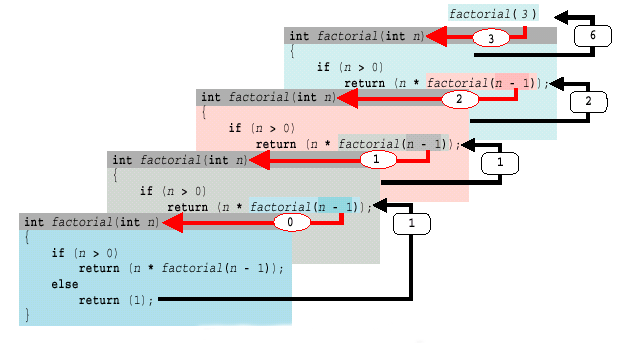
と呼び出します。この際の計算手順を示したのが右図です。
　関数呼出しfactorial(3)によって起動された関数factorial は、仮引数nに3を受け取ります。さて、この関数としては、
　　　　3 * factorial(2)
という値を返したいのですが、この乗算を行うためには、まずfactorial(2)の値を知る必要があります。そこで、2を渡して関数factorial を呼び出します。そうすると、今度はfactorial(1)の値が必要ですから、関数factorial が呼び出されます。
　仮引数nに0を受け取った関数factorial に着目しましょう。nの値は0ですから、即座に1を返すことになり、この関数を呼び出した関数factorial に戻ります。
　その関数factorial は
　　　　1 * factorial(0)
すなわち1 * 1を返し、関数factorial に戻ります。さらに、関数factorial へと戻り、最終的に6が返されることになります。
　このように、何らかの計算・操作を行いたいとき、それを実現するのがたまたま自分自身と同じ関数であれば、その関数を呼び出すことができます。このような関数呼出しを、再帰関数呼出し（recursive function call)といいます。

　階乗値を求める過程を、より視覚的に学習したい方は、ダウンロードのページで《アルゴリズム体験学習プログラム》をダウンロードして実行してみてください。Windows上で動作するプログラムです。

戻る