新・明解Javaで学ぶアルゴリズムとデータ構造

戻る  

演習3-5の解答

２分探索アルゴリズムでは、探索すべきキー値と同じ値をもつ要素が複数存在する場合、それらの要素の先頭要素を見つけるとは限らない。たとえば、以下に示す配列から7を探索すると、中央要素のインデックスである5を見つけることになる。 　２分探索アルゴリズムによって探索に成功した場合（下図ａ）、その位置から先頭側へ走査することによって（下図ｂ）、複数の要素が一致する場合でも、最も先頭側に位置する要素のインデックスを見つけられる。 　そのように改良したメソッドを作成せよ。 　　static int binSearchX (int[] a , int n , int key )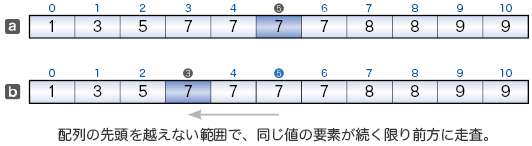

// 演習3-5
// ２分探索（一致する先頭要素を見つける）

import java.util.Scanner;

class BinSearchX {

   //--- 配列aの先頭n個の要素からkeyと一致する要素を２分探索 ---//
   static int binSearchX(int[] a, int n, int key) {
      int pl = 0;            // 探索範囲先頭のインデックス
      int pr = n - 1;      // 　 〃 　末尾のインデックス

      do {
         int   pc = (pl + pr) / 2;   // 中央要素のインデックス
         if (a[pc] == key) {
            for ( ; pc > pl; pc--)   // keyと等しい先頭の要素を探す
               if (a[pc - 1] < key)
                  break;
            return pc;               // 探索成功
         } else if (a[pc] < key)
            pl = pc + 1;            // 探索範囲を前半に絞り込む
         else
            pr = pc - 1;            // 探索範囲を後半に絞り込む
      } while (pl <= pr);

      return -1;               // 探索失敗
   }

   public static void main(String[] args) {
      Scanner stdIn = new Scanner(System.in);

      System.out.print("要素数：");
      int num = stdIn.nextInt();
      int[] x = new int[num];      // 要素数numの配列

      System.out.println("昇順に入力してください。");

      System.out.print("x[0]：");      // 先頭要素の読込み
      x[0] = stdIn.nextInt();

      for (int i = 1; i < num; i++) {
         do {
            System.out.print("x[" + i + "]：");
            x[i] = stdIn.nextInt();
         } while (x[i] < x[i - 1]);   // 一つ前の要素より小さければ再入力
      }

      System.out.print("探す値：");      // キー値の読込み
      int ky = stdIn.nextInt();

      int idx = binSearchX(x, num, ky);   // 配列xから値がkyの要素を探索

      if (idx == -1)
         System.out.println("その値の要素は存在しません。");
      else
         System.out.println("その値はx[" + idx + "]にあります。");
   }
}

戻る