| 第２種情報処理技術者試験 |
1997年度 ＝ 平成9年度・春期 |
午前 |
問9 |
すべての葉をもつ完全２分木がある。この完全２分木で成り立つ関係式はどれか。ここで、nは節点の個数、k（k≧1）は根から葉までの階層数を表す。例の階層数（k）は3である。
例
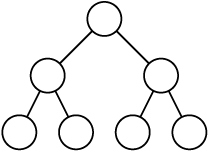
k = 3
| ア n = k(k - 1) + 1
| イ n = k(k - 2) + 3
|
| ウ n = 2k - 1
| エ n = 2k + 1
|
ウ
完全２分木とは、根から下方のレベルへ、同一のレベル内では左から右へノード（節点）が詰められている２分木です。
すなわち、完全２分木は、最も下流側のレベル以外は、すべてノードが詰まっています。また、最下流のレベルは、もちろんすべて詰まっていてもよいのですが、左側から詰められていれば、途中までしかノードがなくても構いません。
木の高さがkである完全２分木がもつことのできるノードは、最大で2k-1となります。
本問で問われているのは、最下流のレベルにノードが詰まっている場合のノード数ですから、最大値である2k - 1となります。
